The proposed framework
Efficient charging infrastructure and operations are crucial to ensure the seamless integration of EVs into the existing transportation system. Figure 2 presents a system designed to improve the optimization of EV charging operations. The proposed model incorporates routing decisions and charging plans for all origin-destination (OD) demands within the transportation network, aiming to enhance the efficiency and convenience of EV charging operations. By considering the remaining energy levels of EVs and accurately estimating the total charging demands of charging stations, the model ensures that EVs are directed to the most suitable charging stations along their routes. This optimization process minimizes travel distance and alleviates anxiety for travelers by providing a reliable and accessible charging infrastructure throughout their journeys. Moreover, the model incorporates setup time and charging time at charging stations to provide a more precise estimation of the overall charging time needed for each EV.
The power sources in the electric charging station are depicted in Fig. 2 by the dashed red line, representing the combination of power grid and renewable energy. Combining renewable energy sources like solar and wind power in electric vehicle charging stations offers a holistic solution. By integrating wind turbines and photovoltaic (PV) cells, these stations can access a reliable and steady energy supply, capitalizing on the synergistic generation profiles of wind and solar power. This synergistic approach optimizes energy generation, effectively utilizing available space, ensuring resilience in diverse weather conditions, enabling load balancing, and facilitating the storage or sale of surplus energy. Incorporating both wind and solar power not only promotes sustainability and decreases carbon emissions but also enhances the public perception of the charging station as a pioneering entity that embraces clean energy for transportation systems.
In the electricity market, suppliers, such as power plants, submit bids indicating the amount of electricity they are willing to supply at various price levels. These bids are typically based on the production costs of the suppliers. The proposed model incorporates an economic perspective by addressing the cost aspect of EV charging operations. It achieves this by considering bidding prices in day-ahead and intra-day electricity markets. By accurately estimating the prices for purchasing electricity at charging stations, the model enables the optimization of charging costs and enhances the efficient utilization of available resources. This advanced approach empowers charging station operators to make well-informed decisions regarding the procurement of electricity. By considering market dynamics and pricing fluctuations, the model assists operators in balancing the cost-effectiveness of charging operations. By providing accurate estimations of bidding prices, the model contributes to the overall cost optimization of EV charging, delivering advantages to both charging station operators and EV owners. With the utilization of these economic insights, stakeholders can enhance the efficiency of their charging operations, minimize expenses, and advance sustainable transportation practices. The model not only supports the growth of the EV market but also facilitates the integration of electric vehicles into the existing energy market ecosystem.
During the bidding process for each hour, a collection of points known as scenarios is utilized on a bidding curve. These scenarios correspond to specific bid prices and bid volumes, providing a comprehensive representation of the various pricing and quantity options offered by suppliers. However, due to the non-linear nature of the formulation resulting from selecting both bid prices and volumes, an approach is taken to linearize the problem. To achieve linearity, the bid prices are treated as fixed exogenous parameters, while the bid volumes are modeled as decision variables. The bidding curve is constructed by interpolating linearly between adjacent price-volume pairs, resulting in a piece-wise linear curve that represents the bids. This linearization simplifies the problem while still capturing the essential characteristics of the bidding process.
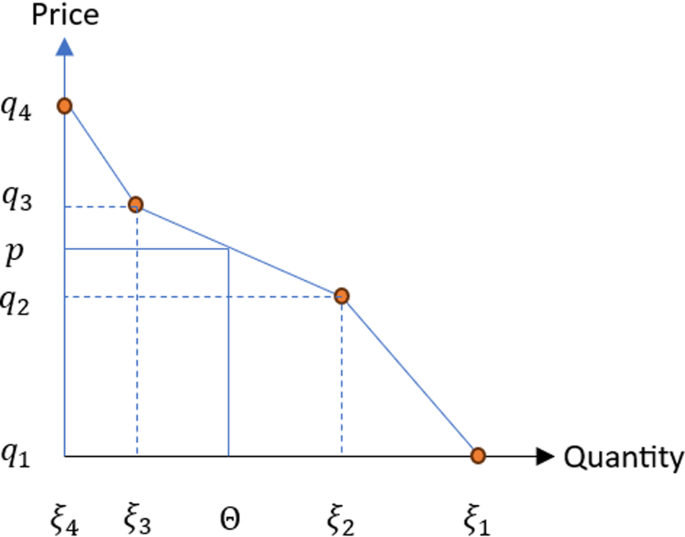
Figure 3 depicts a bidding curve characterized by three line segments, serving as an illustrative example. The bidding curve is typically depicted graphically, with the price plotted on the vertical axis and the quantity on the horizontal axis. Each point on the curve represents a specific price-quantity combination that a supplier is willing to offer. The shape of the curve reflects the supply-side behavior and competitiveness of the market. Equation (1) and Equation (2) represent the bidding curve using different variables. Equation (1) expresses the curve in terms of prices, while Equation (2) expresses it in terms of volumes.
$${p}_{}^{}={q}_{n}+\frac{{q}_{n+1}-{q}_{n}}{{\xi }_{n+1}-{\xi }_{n}}\left(\Theta -{\xi }_{n}\right)\quad if\,{\xi }_{n+1}\le {\Theta }_{}^{}\le {\xi }_{n}\,\forall n\in \left\{1,…,I-1\right\}$$
(1)
$${\Theta }_{}^{}=\frac{{p}_{}^{}-{q}_{n}}{{q}_{n+1}-{q}_{n}}{\xi }_{\left(n+1\right)}^{}+\frac{{q}_{n+1}-{p}_{}^{}}{{q}_{n+1}-{q}_{n}}{\xi }_{n}^{}\quad if\,{q}_{n}\le {p}_{}^{}\le {q}_{n+1}\,\forall n\in \left\{1,…,I-1\right\}$$
(2)
Furthermore, the proposed model takes into account the state of charging for batteries at the charging stations through the consideration of charging and discharging functions. Installing backup power systems, such as batteries, can enable charging stations to continue operating during power outages. These systems can provide electricity to the charging infrastructure, ensuring that electric vehicles can still be charged even when the grid is down. It’s important to properly size and maintain backup power systems to ensure they have sufficient capacity and reliability. By continuously monitoring the charging levels and managing the flow of electricity, the model ensures that the charging stations operate within their capacity limits and prioritize the needs of EVs. This functionality optimizes the charging process, avoiding overloading of the charging infrastructure and maintaining a reliable and stable charging experience for EV owners. The model’s ability to regulate the state of charging at charging stations contributes to the overall efficiency and effectiveness of EV charging operations, enhancing the charging experience and promoting widespread EV adoption. The proposed model aims to generate a set of outputs that collectively contribute to the optimization and improvement of EV charging operations. The outputs derived from the proposed model encompass:
-
The model provides optimized routing decisions for EVs, considering factors such as travel costs, charging station availability, and energy consumption. By optimizing the routes, EVs can reach their destinations efficiently while minimizing energy consumption and charging requirements.
-
The model generates charging plans that determine when and where EVs should charge along their travel routes. By considering the OD demands, the model ensures that there are sufficient charging stations available to meet the charging needs of EVs throughout their journeys.
-
The model takes into account the remaining energy levels of EVs and considers them in the routing and charging decisions. By factoring in the remaining energy, the model aims to reduce traveler anxiety by ensuring that EVs have adequate energy reserves to reach their destinations and avoid running out of charge.
-
The model optimizes the charging demands for charging stations by considering factors such as charging station capacities, electricity grid constraints, and EV charging requirements. This optimization helps in efficiently utilizing the charging infrastructure and minimizing charging congestion.
-
The model considers the availability and variability of renewable energy sources. By optimizing the utilization of these sources, it helps stabilize the power grid. The intermittent nature of renewable energy can be managed by smart charging systems that can adjust charging rates based on the availability of renewable energy, reducing grid stress and balancing electricity supply and demand.
-
Efficient battery management is crucial for optimizing the operation of charging stations. The proposed model facilitates the effective utilization of battery resources by optimizing the charging and discharging functions at charging stations. It considers factors such as station capacity, battery state monitoring, grid integration, energy pricing, and battery health to ensure the efficient utilization of resources, support grid stability, minimize operational costs, and promote the longevity of batteries.
-
The model considers bidding prices for electricity markets to make informed procurement decisions regarding the purchase of electricity for charging operations. By considering market prices, the model aims to optimize the cost-effectiveness of EV charging while ensuring reliable and sustainable energy supply.
By generating these outputs, the proposed model aims to contribute to the optimization and improvement of EV charging operations. This, in turn, promotes the adoption of electric vehicles, fosters the transition to a sustainable transportation system, and helps overcome the challenges associated with the integration of EVs into the existing infrastructure.
Optimal integration model for electric charging stations
In this section, we present an optimization model for electric vehicle charging stations that takes into account renewable energy sources such as photovoltaic (PV) cells and wind turbines. Then, we explore incorporating these renewable energy sources into the proposed model, allowing for a more sustainable and efficient charging infrastructure for electric vehicles. Integrating an optimization model that combines charging and routing plans with the electricity market can indeed help minimize social costs for both users and charging providers. This integrated model can effectively optimize charging and routing plans by considering various factors such as vehicle range, charging infrastructure availability, electricity prices, and user preferences, leading to cost savings and improved efficiency. The model incorporates several factors associated with the value of time, such as travel cost, setup time at the station, and charging duration. By considering these factors, the model provides an accurate assessment of the overall time-related costs involved in charging at a charging station.
The first element of the objective function incorporates the expenditure associated with purchasing electricity from both the day-ahead and intra-day electricity markets. We incorporate scenarios that are generated using probability distributions for bid prices. This approach allows us to explore a range of potential situations that could occur during a bidding process. Rather than relying on a singular fixed bid price, we consider the probabilities associated with different bid prices, thereby taking into account the likelihood of various bid prices arising. The second component denotes the travel time from point O to point D, assuming a consistent speed. The third component of the objective function accounts for the cumulative time spent on setup at each station. The last component corresponds to the duration of charging at the station. The notations used in the proposed framework are provided in Table 1.
$$\begin{array}{rcl}{{{\rm{Min}}}}Z&=&\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{s}\mathop{\sum}\limits_{t}{\theta }_{s}\left({p}_{its}^{ID}{\Theta }_{its}^{ID}+{p}_{its}^{DA}{\Theta }_{its}^{DA}\right)+\mathop{\sum}\limits_{i}\mathop{\sum }\limits_{j}\mathop{\sum}\limits_{t}\mathop{\sum }\limits_{k}\mathop{\sum }\limits_{v}\frac{{d}_{ij}{x}_{ijtkv}}{{\upsilon }_{ijtkv}}\\ &+&\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{t}\mathop{\sum }\limits_{k}\mathop{\sum }\limits_{v}^{}{u}_{it}{y}_{itkv}+\mathop{\sum}\limits_{i}\mathop{\sum }\limits_{t}\mathop{\sum }\limits_{k}\mathop{\sum }\limits_{v}{\pi }_{it}{b}_{itkv}\end{array}$$
(3)
Constraints (4) and (5) in this context serve as a condition related to the inclusion of a specific arc (i, j) in the path. When the decision variable xijtkv (representing the inclusion of arc (i, j) in the path) is equal to 1, it means that the arc is indeed included in the path. In this scenario, constraint (4) becomes active and imposes a requirement on the variables ajtkv, aitkv, bitkv, and dij14.
$${a}_{jtkv}\ge {a}_{itkv}+{b}_{itkv}-{d}_{ij}-M\left(1-{x}_{ijtkv}\right)\,\forall i,j\in N,\forall t\in T,\forall k\in K,\forall v\in V$$
(4)
On the other hand, if xijtkv is equal to 0, indicating that the arc (i, j) is not included in the path, constraints (4) and (5) become redundant. In this case, it does not contribute any additional information or place any additional constraints on the variables. It effectively becomes inactive and does not affect the optimization problem14.
$${a}_{jtkv}\le {a}_{itkv}+{b}_{itkv}-{d}_{ij}+M\left(1-{x}_{ijtkv}\right)\,\forall i,j\in N,\forall t\in T,\forall k\in K,\forall v\in V$$
(5)
Constraints (6), (7), and (8) play a vital role in maintaining the flow balance equation within the transportation network problem. Constraint (6) ensures that the flow of electric vehicles into the set of source nodes \(O\left(k\right)\) is equal to the flow out of it, while
$$\mathop{\sum }\limits_{i=1}^{N}{x}_{ijtkv}-\mathop{\sum }\limits_{i=1}^{N}{x}_{jitkv}=-1\,\forall k\in K,\forall j\in O\left(k\right),\forall t\in T,\forall v\in V$$
(6)
Constraint (7) extends this requirement to all intermediate nodes, ensuring that the flow into and out of each intermediate node is balanced.
$$\mathop{\sum }\limits_{i=1}^{N}{x}_{ijtkv}-\mathop{\sum }\limits_{i=1}^{N}{x}_{jitkv}=0\,\forall k\,\in\, K,j\,\ne \,O\left(k\right),j\ne D\left(v\right),\forall t\in T,\forall v\in V$$
(7)
Constraint (8) ensures a similar balance for the set of destination nodes \(D\left(k\right)\), enabling the network to maintain flow balance and integrity while designating the set \(O\left(k\right)\) as source nodes, nodes in \(D\left(k\right)\) as destination nodes, and the remaining nodes as intermediaries. This structural enforcement preserves the network’s functionality and integrity.
$$\mathop{\sum}\limits_{i=1}^{N}{x}_{ijtkv}-\mathop{\sum }\limits_{i=1}^{N}{x}_{jitkv}=1\,\forall k\in K,\forall j\in D\left(k\right),\forall t\in T,\forall v\in V$$
(8)
Constraint (9) specifies that the charging amount at node i should not exceed the charging capacity (δ) minus the remaining charge level at that node.
$${b}_{itkv}\le \delta -{a}_{itkv}\,\forall i\in N,\forall t\in T,\forall k\in K,\forall v\in V$$
(9)
Constraint (10) states that the charging amount at node i is the difference between the charging capacity and the charge adjustment at that node. To prevent overcharging beyond the available capacity of the battery, a parameter ritkv is used to calibrate the amount of charge replenished at a site. This is achieved by satisfying the inequality δyitkv − ritkv ≤ δ − aitkv (where bitkv in Constraint (9) is replaced by δyitkv − ritkv in Constraint (10)). Ideally, the desired formula would be δyitkvL ≤ δ − aitkv, where L is a recharging coefficient ranging of 0-1, based on the available capacity of the battery at each stop. The recharging coefficient regulates the amount of charge replenished at a specific site. However, solving this nonlinear equation is currently challenging. Therefore, we introduce a linear formula with an adjustment variable ritkv to approximate the desired behavior18.
$${b}_{itkv}=\delta {y}_{itkv}-{r}_{itkv}\,\forall i\in N,\forall t\in T,\forall k\in K,\forall v\in V$$
(10)
Constraint (11) establishes a direct relationship between the inclusion of a node in the path and the possibility of charging at that node. It stipulates that charging at a particular node can occur if and only if that node is included in the travel path14.
$${y}_{itkv}\le \mathop{\sum }\limits_{j}{x}_{jitkv}\,\,\forall i\in Z,\forall t\in T,\forall k\in K,\forall v\in V$$
(11)
Constraint (12) implies that the EV is fully charged at the starting point18.
$${a}_{itkv}=\delta ,\forall i\in O\,\left(k\right),\,\forall t\in T,\forall k\in K,\forall v\in V$$
(12)
The bidding curves enable the efficient allocation of electricity resources by facilitating the matching of supply and demand at equilibrium prices. Equation (13) formulates the bidding curve for the day-ahead market. This curve describes the relationship between the bid price and the corresponding quantity of electricity that market participants are willing to supply or demand in the day-ahead market. It helps determine the market clearing price and quantity for the day-ahead market29,30.
$${\Theta }_{its}^{DA}=\frac{{p}_{its}^{DA}-{q}_{n}}{{q}_{n+1}-{q}_{n}}{\xi }_{\left(n+1\right)ti}^{DA}+\frac{{q}_{n+1}-{p}_{its}^{DA}}{{q}_{n+1}-{q}_{n}}{\xi }_{nti}^{DA}if\,\,{q}_{n}\le {p}_{its}^{DA}\le {q}_{n+1}\,\forall i\in Z,\forall t\in T,\forall n,s\in \left\{1,…,I-1\right\}$$
(13)
Equation (14) formulates the bidding curve for the intra-day market. This curve represents the price-quantity relationship for electricity bids in the intra-day market. It reflects the willingness of market participants to buy or sell electricity at different prices in the intra-day market, allowing the determination of the market clearing price and quantity for intra-day transactions. By formulating these bidding curves, market participants can express their preferences and strategies for buying or selling electricity at different price levels29,30.
$$\begin{array}{l}{\Theta }_{its}^{ID}=\frac{{p}_{its}^{ID}-{q}_{n}}{{q}_{n+1}-{q}_{n}}{\xi }_{\left(n+1\right)tis}^{ID}+\frac{{q}_{n+1}-{p}_{its}^{ID}}{{q}_{n+1}-{q}_{n}}{\xi }_{ntis}^{ID}\,if\,{q}_{n}\le {p}_{its}^{ID}\\\qquad\le {q}_{n+1}\,\forall i\in Z,\forall t\in T,\forall n,s\in \left\{1,…,I-1\right\}\end{array}$$
(14)
Constraint (15) in the day-ahead market ensures that the bidding curve submitted by market participants follows a non-increasing pattern. This means that as the quantity of electricity increases, the corresponding bid prices must decrease or remain the same. This rule helps maintain fairness and efficiency in the day-ahead market by discouraging participants from artificially inflating prices as the quantity increases.
$${\xi }_{\left(n+1\right)ti}^{DA}\le {\xi }_{nti}^{DA}\,\forall i\in Z,\forall t\in T,\forall n\in \left\{1,…,I-1\right\}$$
(15)
In the intra-day market, Constraint (16) serves a similar purpose but with a slight difference. The bidding curves in the intra-day market are based on the realized scenario from the day-ahead market. This means that the bidding volume in the intra-day market is influenced by the specific conditions and outcomes observed in the day-ahead market. The scenario index is introduced to reflect these conditions and ensure that the bidding curve remains non-increasing within the context of the realized scenario.
$${\xi }_{\left(n+1\right)tis}^{ID}\le {\xi }_{ntis}^{ID},\,\forall t,\,\forall i\in Z,\forall t\in T,\forall n,s\in \left\{1,…,I-1\right\}$$
(16)
Equation (17) is a critical component in maintaining power balance within the sequential markets. It establishes the requirement that the combined power purchased from both the day-ahead and intra-day markets must equal the dedicated power allocation designated for charging electric vehicles and charging the battery. This equation ensures that the total power procured from the markets aligns precisely with the power demand necessary for the specific tasks of electric vehicle charging and battery charging.
$${\Theta }_{its}^{DA}+{\Theta }_{its}^{ID}={\Theta }_{its}^{V}+{\Theta }_{its}^{C}\,\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(17)
Constraint (18) effectively meets the power demand of the charging station by considering both the purchased power and the power discharged from the battery for electric vehicle charging. The equation accounts for the combined power from these sources to ensure that the station’s charging requirements are adequately fulfilled.
$${\Theta }_{its}^{V}+{\Theta }_{its}^{D}=\mathop{\sum }\limits_{v}\mathop{\sum }\limits_{k}{\rho }_{e}{b}_{itkv}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(18)
where ρe is the energy consumption rate per kilometer, which converts the distance to energy.
The charging equation establishes a relationship between the charge current, \({I}_{its}^{c}\) (measured in amperes, A), the charge power, \({\Theta }_{its}^{C}\), and the state of charge (SOC) of the battery. In this equation, Vi represents the battery voltage, which is a measure of the electrical potential difference across the battery terminals. The term \({\eta }_{i}^{C}\) denotes the charging efficiency, which accounts for any energy losses that occur during the charging process. Hence, it can be represented as:
$${I}_{its}^{C}=\frac{{\Theta }_{its}^{C}}{{V}_{i}{\eta }_{i}^{C}}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(19)
By dividing the charge power, \({\Theta }_{its}^{C}\), by the product of the battery voltage, V, and the charging efficiency, \({\eta }_{i}^{C}\), the charging equation determines the charge current required to deliver the specified charge power to the battery.
During the discharging process, the battery releases stored energy to power an external load. The discharge current, denoted as \({I}_{its}^{D}\), represents the rate at which electrical charge flows out of the battery and is typically measured in amperes (A). This equation shows that the discharge current is equal to the discharge power divided by the product of the battery voltage and the efficiency of the discharge process.
$${I}_{its}^{D}=\frac{{\Theta }_{its}^{D}}{{V}_{i}{\eta }_{i}^{D}}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(20)
The change in SOC over time can be calculated based on the charge and discharge currents. Equation (21) represents the net charge or discharge during the time interval, divided by the battery capacity. Assuming a small time interval Δt, the change in SOC, ΔSOC, can be expressed as:
$$\Delta SO{C}_{its}=\frac{\left({I}_{its}^{C}-{I}_{its}^{D}\right)\Delta t}{{Q}_{i}}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(21)
To update the State of Charge (SOC) of a battery, the initial SOC is modified based on the change in SOC. The updated SOC (SOCits) is obtained by adding the change in SOC (ΔSOC) to the initial SOC. This calculation helps track the battery’s energy level and reflects any charge or discharge that has occurred. By continuously updating the SOC, it becomes possible to monitor the battery’s remaining capacity, estimate runtime, and optimize charging and discharging strategies.
$$SO{C}_{its}=SO{C}_{i\left(t-1\right)s}+\Delta SO{C}_{its}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(22)
Maintaining the State of Charge within the recommended range of \(SO{C}_{its}^{Min}\) to \(SO{C}_{its}^{Max}\) is essential for optimal battery performance, longevity, and safe operation. \(SO{C}_{its}^{Max}\) defines the maximum allowable level of charge for a battery, beyond which overcharging may occur, leading to potential damage and safety risks. \(SO{C}_{its}^{Min}\), on the other hand, represents the minimum acceptable level of charge to avoid deep discharge, which can cause irreversible damage and loss of capacity.
$$SO{C}_{its}^{Min}\le SO{C}_{its}\le SO{C}_{its}^{Max}\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(23)
Constraints (24) and (25) sets the nonnegativity and the binary condition of the variables.
$$\begin{array}{rcl}&&{b}_{itkv}\ge 0;{a}_{itkv}\ge 0;{r}_{itkv}\ge 0;{\Theta }_{its}^{ID}\ge 0;{\Theta }_{its}^{DA}\ge 0;{\xi }_{ntis}^{ID}\ge 0;\\ &&{\xi }_{nti}^{DA}\ge 0;{\Theta }_{its}^{C}\ge 0;{\Theta }_{its}^{D}\ge 0,\,\forall i\in N,\forall t\in T,\forall k\in K,\forall v\in V,\forall s\in \left\{1,…,I-1\right\}\end{array}$$
(24)
$${y}_{itkv}\in \left\{0,1\right\};{x}_{ijtkv}\in \left\{0,1\right\}\,\forall i\in N,\forall t\in T,\forall k\in K,\forall v\in V$$
(25)
Modeling of wind turbine
To model wind turbines in charging stations for electric vehicles, it is necessary to comprehend the principles of wind energy conversion and its connection to power generation. A widely employed mathematical model for this purpose is the power curve model. This model establishes a relationship between the wind speed and the power output of the turbine. The power output (\({\Theta }_{it}^{W}\)) of a wind turbine can be represented using the following equation40,41:
$${\Theta }_{it}^{W}=0.5{\rho }_{it}{A}_{i}{C}_{i}^{p}{\left({V}_{it}^{w}\right)}^{3}\,\forall i\in Z,\forall t\in T$$
(26)
where ρit represents the air density, Ai is the swept area of the rotor, \({C}_{i}^{p}\) is the power coefficient that quantifies the turbine’s efficiency, and \({V}_{it}^{w}\) denotes the wind speed. By employing this equation, one can determine the wind turbine’s power output based on the prevailing wind conditions.
Modeling of PV array
To model photovoltaic (PV) arrays in charging stations for electric vehicles, it is essential to utilize mathematical representations that accurately capture the conversion of solar energy into electrical power. One prevalent approach involves employing the single-diode model, which effectively describes the current voltage (I-V) characteristics of the PV array. The single-diode model represents the I-V relationship of a PV module or array using the following equation41,42:
$${I}_{it}^{S}={I}_{it}^{ph}-{I}_{it}^{0}\left(\exp \left(\frac{{V}_{it}^{s}+{I}_{it}^{S}\cdot {R}_{it}^{s}}{n\cdot {V}_{it}^{th}}\right)-1\right)-\frac{{V}_{it}^{s}+{I}_{it}^{S}\cdot {R}_{it}^{s}}{{R}_{it}^{sh}}\,\forall i\in Z,\forall t\in T$$
(27)
The mathematical model for a photovoltaic cell involves several parameters that describe its electrical behavior. In this model, the cell’s output current (\({I}_{it}^{S}\)) is related to its output voltage (\({V}_{it}^{s}\)) through various factors. These factors include the photocurrent generated by the cell under illumination (\({I}_{it}^{ph}\)), the reverse saturation current (or dark current) of the cell (\({I}_{it}^{0}\)), the series resistance of the cell (\({R}_{it}^{s}\)), the diode ideality factor (n), and the thermal voltage (\({V}_{it}^{th}\)). The thermal voltage is calculated as the product of Boltzmann’s constant (Bk), the temperature in Kelvin (Ts), and the elementary charge (q). Additionally, the model accounts for the shunt resistance of the cell (\({R}_{it}^{sh}\)). Together, these parameters provide insights into the electrical characteristics and performance of the photovoltaic cell.
The power (\({\Theta }_{it}^{S}\)) generated by a photovoltaic (PV) cell can be calculated by multiplying the current (\({I}_{it}^{S}\)) generated by the cell with the voltage (\({V}_{it}^{S}\)) across its terminals. Mathematically, it can be expressed as:
$${\Theta }_{it}^{S}={I}_{it}^{S}{V}_{it}^{S}\,\forall i\in Z,\forall t\in T$$
(28)
To incorporate renewable energy sources, specifically solar and wind, for charging stations, we modify Equation (17). Other formulations remain unchanged. The updated equation now reflects the contribution of solar and wind energy to power the charging stations. The equation is as follows:
$${\Theta }_{its}^{DA}+{\Theta }_{its}^{ID}+{\Theta }_{it}^{S}+{\Theta }_{it}^{W}={\Theta }_{its}^{V}+{\Theta }_{its}^{C}\,\,\forall i\in Z,\forall t\in T,\forall s\in \left\{1,…,I-1\right\}$$
(29)
In equation (29), the left-hand side represents the combined power purchased from both the day-ahead (DA) and intra-day (ID) markets, as well as the renewable energy provided by solar (S) and wind (W). The right-hand side represents the dedicated power allocation designated for charging electric vehicles (V) and charging the battery (C). This equation ensures that the total power procured from the markets aligns precisely with the power demand necessary for the specific tasks of electric vehicle charging and battery charging.