Math Puzzle: How Many Routes Can You Find?
Try to solve a traveling salesman’s directional dilemma
Henry Ernest Dudeney may be among the most significant puzzle inventors who ever lived. He was born in Mayfield, England, in 1857, the son of a village schoolteacher, and he died in 1930. Dudeney designed brainteasers for newspapers and magazines regularly for decades, and he later compiled most of his puzzles into books. This head-scratcher comes from his 1917 book Amusements in Mathematics.
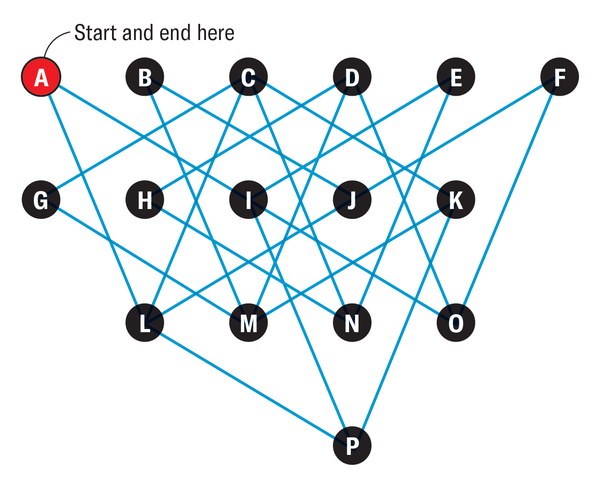
A traveling salesman who lives in city A wants to visit all cities from B to P over the course of a week, though not necessarily in alphabetical order, and return to A at the end. He plans to enter each city exactly once. The blue lines are the only roads connecting the 16 cities. The traveling salesman may use only a straight route between any two cities; he is not allowed to turn at the intersection of two streets. How many different routes are possible?
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

If the traveling salesman enters a city on one road, he must leave it again on another. In order for a round trip to be possible at all, at least two roads must lead to each city. There are exactly two roads leading to cities A, B, E, F, G and H. The traveling salesman must therefore travel on these roads no matter what. This also determines which roads he will use to reach and leave cities I, J, M and N. The remaining connections are then also clear. There is therefore only one possible round trip for the traveling salesman—AIENHDOFJBMGCKPLA—but he can travel it in two different directions.
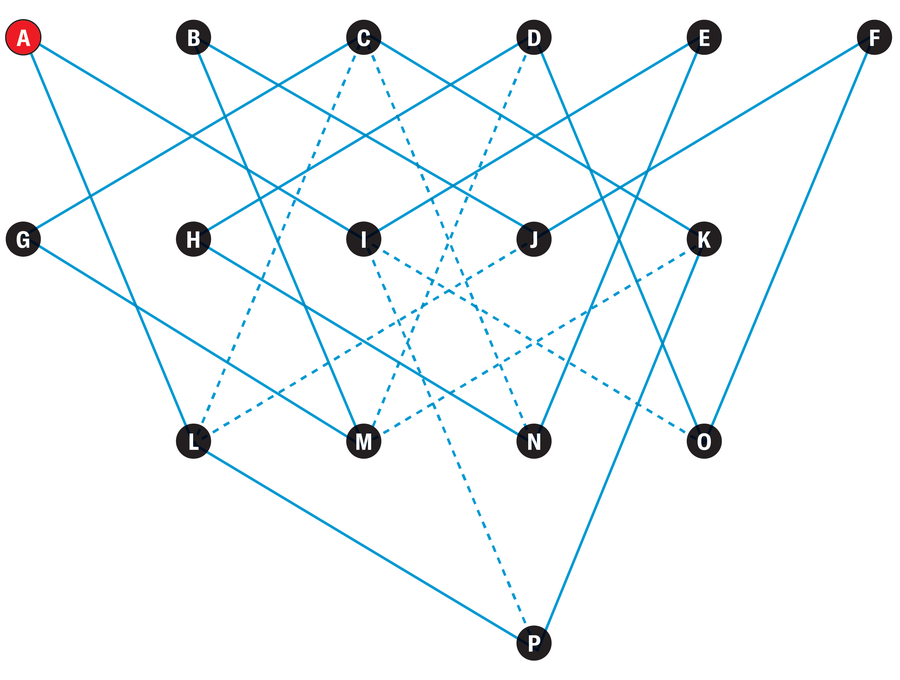
Editor’s Note: The version of the puzzle that appeared in the print edition of the July/August 2024 issue incorrectly included connections between C and I and between I and M. The error did not impact the solution.